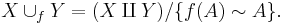Adjunction space

In mathematics, an adjunction space (or attaching space) is a common construction in topology where one topological space is attached or "glued" onto another. Specifically, let X and Y be a topological spaces with A a subspace of Y. Let f : A → X be a continuous map (called the attaching map). One forms the adjunction space X ∪_f Y by taking the disjoint union of X and Y and identifying x with f(x) for all x in A. Schematically,

Sometimes, the adjunction is written as 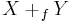. Intuitively, we think of Y as being glued onto X via the map f.

As a set, X ∪_f Y consists of the disjoint union of X and (Y − A). The topology, however, is specified by the quotient construction. In the case where A is a closed subspace of Y one can show that the map X → X ∪_f Y is a closed embedding and (Y − A) → X ∪_f Y is an open embedding.

Examples

• A common example of an adjunction space is given when Y is a closed n-ball (or cell) and A is the boundary of the ball, the (n−1)-sphere. Inductively attaching cells along their spherical boundaries to this space results in an example of a CW complex.
• Adjunction spaces are also used to define connected sums of manifolds. Here, one first removes open balls from X and Y before attaching the boundaries of the removed balls along an attaching map.
• If A is a space with one point then the adjunction is the wedge sum of X and Y.
• If X is a space with one point then the adjunction is the quotient Y/A.

Categorical description

The attaching construction is an example of a pushout in the category of topological spaces. That is to say, the adjunction space is universal with respect to following commutative diagram:

Here i is the inclusion map and φ_X, φ_Y are the maps obtained by composing the quotient map with the canonical injections into the disjoint union of X and Y. One can form a more general pushout by replacing i with an arbitrary continuous map g — the construction is similar. Conversely, if f is also an inclusion the attaching construction is to simply glue X and Y together along their common subspace.

See also

• Quotient space

References

• Stephen Willard, General Topology, (1970) Addison-Wesley Publishing Company, Reading Massachusetts. (Provides a very brief introduction.)
• Adjunction space on PlanetMath